
All irrational numbers can be written as continued fractions, like the one below.
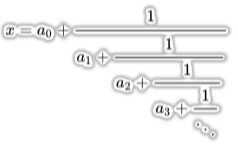
It turns out that, as N approaches infinity, the geometric mean of the first N a_i coefficients converges to a constant called Khinchin's constant for almost all (i.e., all but a Lebesgue null set of) numbers. This property can be called Khinchin;s property.
Although almost all numbers have this property, and some well-known constants are believed to have it, there are no natural examples of numbers that have been proven to have it. This includes the question of whether Khinchin's constant itself has the property.
Note that in order to have the property, a number must be irrational, so this market can only resolve YES if /JosephNoonan/is-khinchins-constant-irrational resolves YES.